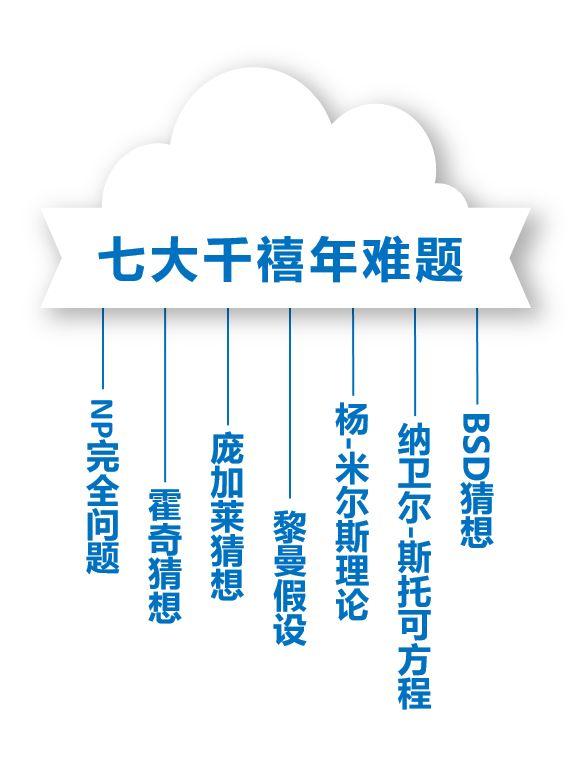
十大无解数学题及答案（世界十大数学难题）

1.哥德巴赫猜想

1742 年的时候，数学家哥德巴赫提出来，只要是比 2 大的偶数，都能写成两个质数相加。就像 4 等于 2 加 2，6 等于 3 加 3，8 等于 3 加 5 之类的。但是到现在也没完全证明出来。这个猜想要是能证明了，对数论和数学分析那些领域影响可大了。哥德巴赫猜想那可是被叫做 “数学皇冠上的明珠”。不过呢，这哥德巴赫猜想太难证明了，很长时间都弄不出来，就让一些人对数学研究的进展有点怀疑了。而且还有些不专业的人瞎试，弄出些错的证明，给数学界带来点乱子。

2.费马大定理

17 世纪的时候，法国那个数学家费马提出来：没有三个比 1 大的整数 a、b 和 c，能让 a 的 n 次方等于 b 的 n 次方加上 c 的 n 次方（n 大于 2）。这个定理的证明过程可长了，好几个世纪，一直到 1995 年，英国那个数学家安德鲁・怀尔斯才给出个完整的证明。这一证明，给数学研究提供了新的办法和思路。费马大定理被叫做 “近代三大数学难题之一”。但是在这很长的证明过程里，好多数学家花了可多时间和精力，结果什么也没弄成，这在一定程度上就让一些搞研究的人有点没积极性了。而且找证明的时候，还走了些错路，浪费不少资源。

3.黎曼猜想

1859 年的时候，德国那个数学家黎曼提出来的，这个猜想是关于素数怎么分布的问题，就是假设黎曼 ζ 函数的那些不是平凡的零点都在复平面的临界线上。这个对解析数论、代数数论还有数学物理那些个领域可重要了，虽然好多数学家都试过，但是到现在也没个大突破。黎曼猜想被叫做 “纯数学领域最重要的未解难题之一”。黎曼猜想一直没解决，就让相关领域的研究有点受限制了。有些研究是建立在黎曼猜想成立的基础上的，要是最后黎曼猜想被证明不成立，那这些研究就得重新弄了。

4.庞加莱猜想

这个猜想是关于几何形状的基本问题，就是假设在三维空间里，随便一个封闭的三维形状都能连续地变成一个球。经过好多数学家努力，最后在 2003 年被证明了，这一证明对理解三维空间的性质可重要了。庞加莱猜想被叫做 “世纪难题”。不过在证明庞加莱猜想的过程里，也有点争议。有些数学家对这个证明的完整性和正确性有点怀疑，这在一定程度上就影响了数学界对这个成果的认可程度。

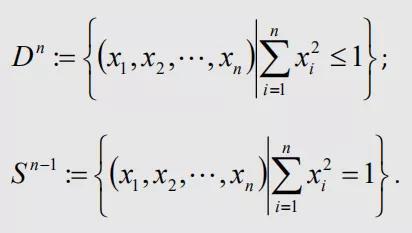
5.纳维尔 - 斯托克斯方程的存在性与光滑性

纳维尔 - 斯托克斯方程是描述流体咋运动的一个基本方程。这个方程解的存在性和光滑性问题一直是数学和物理学领域没解决的难题，好多数学家都试过，但是现在也没啥决定性的进展。要是能解决这个问题，就能更好地理解流体运动的规律。纳维尔 - 斯托克斯方程的存在性与光滑性问题被叫做 “七大千禧年难题之一”。这个难题一直没解决，就让流体力学那些相关领域的理论发展有点受阻碍了。而且因为不知道解到底存不存在、光不光滑，在实际工程应用里也有点风险和不确定的地方。

6.杨 - 米尔斯存在性和质量间隙

杨 - 米尔斯理论是粒子物理学里的基本理论，说的是基本粒子怎么相互作用。但是关于杨 - 米尔斯存在性和质量间隙这个问题一直是数学物理领域的难题，涉及到量子场论和微分几何的深层次联系。要是能解决这个问题，就能更好地理解基本粒子的性质和行为。杨 - 米尔斯存在性和质量间隙问题被叫做 “理论物理学的重大难题”。这个问题太难了，就让理论物理学的发展有点受限制了。而且因为对质量间隙理解得不深，在一些高能物理实验的设计和解释上也有点难。

7.贝赫和斯维讷通 - 戴尔猜想

这个猜想是关于椭圆曲线和模形式的问题，就是假设对于随便一个给定的整数 k，都有有限多个椭圆曲线，能让它的 L 函数在 s 等于 k 的时候值不是零。这个对代数几何和数论那些领域可重要了，要是能解决这个问题，就能更好地理解椭圆曲线和模形式的性质。贝赫和斯维讷通 - 戴尔猜想被叫做 “重要的数论难题”。这个猜想没解决，就让数论领域的一些研究不好往深处弄。而且因为这个猜想挺复杂，有些错的尝试可能会误导别的研究者。

8.霍奇猜想

这是关于代数几何的基本问题，涉及到代数曲面的几何性质。就是假设对于随便一个不是奇异的复射影代数曲面，它的霍奇线都是代数的。要是能解决这个问题，就能更好地理解代数曲面的几何结构，推动代数几何领域发展。霍奇猜想被叫做 “代数几何的重大难题”。霍奇猜想太难攻克了，就让代数几何的一些分支发展有点受限制。而且在试着证明的过程里，可能会有一些错的思路，影响研究者的信心。

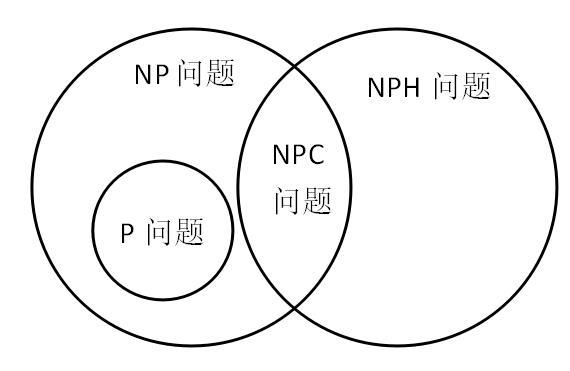
9.P 对 NP 问题

这个问题涉及到计算的复杂性和算法的效率。P 类问题就是有多项式时间算法的问题，NP 类问题就是能在多项式时间里验证解的问题。P 对 NP 问题就是假设所有 NP 问题都是 P 问题，也就是所有能在多项式时间里验证解的问题都有多项式时间算法。要是能解决这个问题，就能更好地理解计算复杂性的本质，推动计算机科学和数学领域发展。P 对 NP 问题被叫做 “计算理论的核心难题”。要是 P 对 NP 问题很长时间解决不了，可能会影响计算机科学领域一些关键问题的解决，像密码学、优化问题之类的。而且在研究的过程里，可能会因为方向不对浪费好多资源。

10.BSD 猜想

这个猜想是关于椭圆曲线和有限域的问题，涉及到椭圆曲线的算术性质和几何性质的联系。就是假设对于随便一个给定的椭圆曲线 E 和有理数 d，如果 L（E，d）不等于 0，那就存在阶为 d 的 E 的有理点。要是能解决这个问题，就能更好地理解椭圆曲线的算术性质和几何性质，推动数论和代数几何领域发展。BSD 猜想被叫做 “数论中的重要难题”。BSD 猜想没解决，就让数论和代数几何领域的一些研究不好有大突破。而且在试着证明的过程里，可能会有一些错的方法，影响研究的进展。