数字的来历及演变过程

数字伴随着人类社会的出现而出现，古时候人类为了便于记事，会在绳子上打个小结，又刚好人类有两个手，每个手有五个手指。最初产生了1、2、3、4、5、6、7、8、9、10这样的正整数。上古时期每个文明都发现了数字，只是阿拉伯数字最容易进行计数，以至于现在国际通行阿拉伯数字，不过阿拉伯数字不是阿拉伯人发明的，而是有印度人发明阿拉伯人把它传给了世界。

0的产生要到很久以后了，之前人们用空来表示0，但是很不方便，偶然的机会0这个数字产生了。这是数字由正整数扩充到了0，0不是正整数它是最小的自然数。
随着人类社会的发展，商业开始出现，在使用数字时人们发现，当用1头猪换10只鸡时，如果别人没有10只只有8只，就记作欠两只，欠两只就是负整数。负数出现的更晚，直到和牛顿同时发现微积分的莱布尼茨还不认可负数。负整数和自然数（0和正整数）共同构成了整数。
数字的运算随着数字产生而产生，开始只是加减运算，对于较大重复累加的数字，加法显得特别麻烦，乘除应运而生。分数进入历史舞台，整数和分子分母都是整数的分数都有其具体形态，我们现在称之为有理数。
无理数的诞生是数字发现史中最悲惨的，古时候有一个毕达哥拉斯学派，他们认为万物皆数，毕达哥拉斯定理就是他发现的，就是我们学的勾股定理。他有一个学生希帕索斯在研究正方形的时候，如果边长是1，它的对角线的长度应该是√2，假设√2=a/b，则a、b同为整数且不可再约分，两边同时平方2=a^2/b^2，得出a^2=2*b^2，这时a^2一定是偶数a，也是偶数，且a^2能被4整除，两边同时约掉2，那么b^2是偶数，b也是偶数，至此a、b同时是偶数与假设不可约分相矛盾，进而√2不是任何两个整数的比。这与毕达哥拉斯的万物皆数相矛盾。无理数被发现，最后希帕索斯被无情的抛于大海中。
1844年著名数学家刘维尔写出了下面这样一个无限小数，a=
0.110001000000000000000001000…（a=1/10^1!+1/10^2!+1/10^3!+…），并且证明a不可能满足任何整系数代数方程，由此证明了它不是一个代数数。超越数被发现，超越数有无穷多个，但目前为止发现的超越数极其少，因为要证明一个数是超越数是很难的。著名的π和e都是超越数。所有的超越数都是无理数，实代数数、实超越数共同组成了实数，当然有理数和无理数也共同组成了实数。另外超越数的发现间接证明了尺规画圆问题。

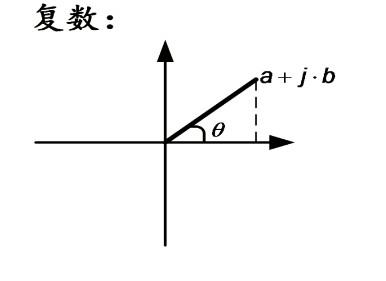
在解一元三次方程时，人们发现一元三次方程有三个解，大部分情况下会出现开负数平方。17世纪著名数学家、哲学家笛卡尔首先引进了虚数，后来人们用i来表示虚数单位。虚数i=√-1，完美解决了开负数平方的问题。实数和虚数共同组成了复数a+bi，当b等于0时，a+bi是实数，其它情况都是虚数，其中当a等于0时称为纯虚数。如果把复数放到坐标系内，我们会发现，实数只能有一条线a轴，纯虚数有一条线bi轴，复数却是整个平面。

数字的扩充到复数就告别了一段落，目前为止人类发现的最高等级数就是复数。重温一下数字发现的历程，加法的需要发现了正整数，减法的需要发现了0和负整数，除法的需要发现了分数，至此有理数全部到位。开方计算发现了无理数，偶然机会发现了超越数，实数全部到位。因为其它计算的需求发现了虚数，虚数和实数共同组成了复数，并建立了复平面坐标系。
延伸讲个小猜想，数字还会扩充吗？实数轴和每个实数都是一一对应关系，并且任何两个不相等的实数其中间必定有一个数。个人认为这是一个悖论，假设实数a和b是两个不同且紧紧相邻的实数，则a和b中间只有一个数设为c，那么c这个数非常神奇，a和c、c和b一定是互不相等的数，但是它们中间不再有任何实数分布！所以0.9999……不等于1，哈哈哈！我不是民科，这个东西我还是不敢去推翻的。

前段时间看了一部科幻电影，说的是超光速飞行是很简单的，导致很多宇宙文明都发现了，地球人却错过了一次次的机会，但因祸得福，我们的科学技术均衡发展，其他宇宙文明却被超光速飞行羁绊了其它科学技术。最终要来地球要饭吃。所以，我刚才的实数悖论会不会是被微积分给羁绊了思想？数字已经由线发展到面，会不会发展到三维？